Here, we will derive the Fourier Transform formula ourselves, from scratch, which is:

$$A(\omega) = \int_{-\infty}^{+\infty} f(x)e^{-i\omega x}dx$$

Don’t be scared; it will be much easier than you imagine. After that, we can dive into the fast version of it. They are pretty similar.

Step 1: Integral

---

We know that we have to evaluate these waves. If the evaluation results are correlated with each other, we can say these two waves are correlated (one of them is a component of another).

Previously, we were picking peak points for this evaluation. But we might as well have picked any periodical point. Because, recall, our aim was to see how much candidate and complex wave are related.

In fact, it would be even better if we are to evaluate the complex wave at every point of the candidate wave. This would have been too much of a hassle; that’s why we went with periodical points. Now, we can be more hardcore.

There are infinite points in a wave, right? How to add infinite points?

A good mathematical approach for that would be taking the integral of the candidate wave and comparing the result with the complex wave. Taking the integral of a function means finding their area with respect to the x-axis. See the image below:

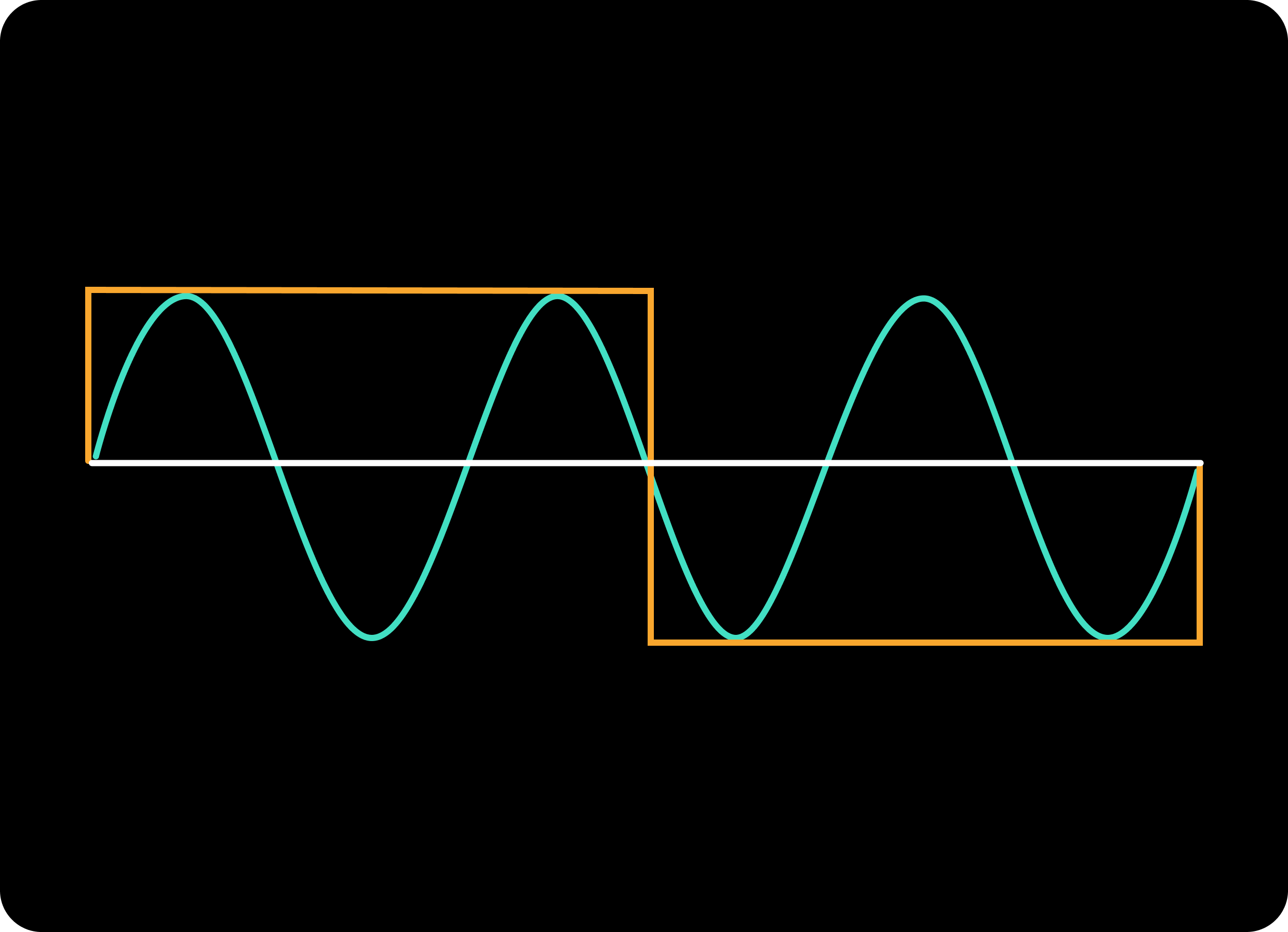
We have two waves here:

• Orange one is the complex wave (the square one). Yes, waves can be square too.
• Cyan one is a basic sin wave.

Let’s inspect the left part of the image:

Orange wave is positive on average on the left part.

Yes, it is not only on average, but always positive. However, we only care for the average (or sum) here.

And if we inspect Cyan wave, we also see it is positive on average.

Now, the right part:

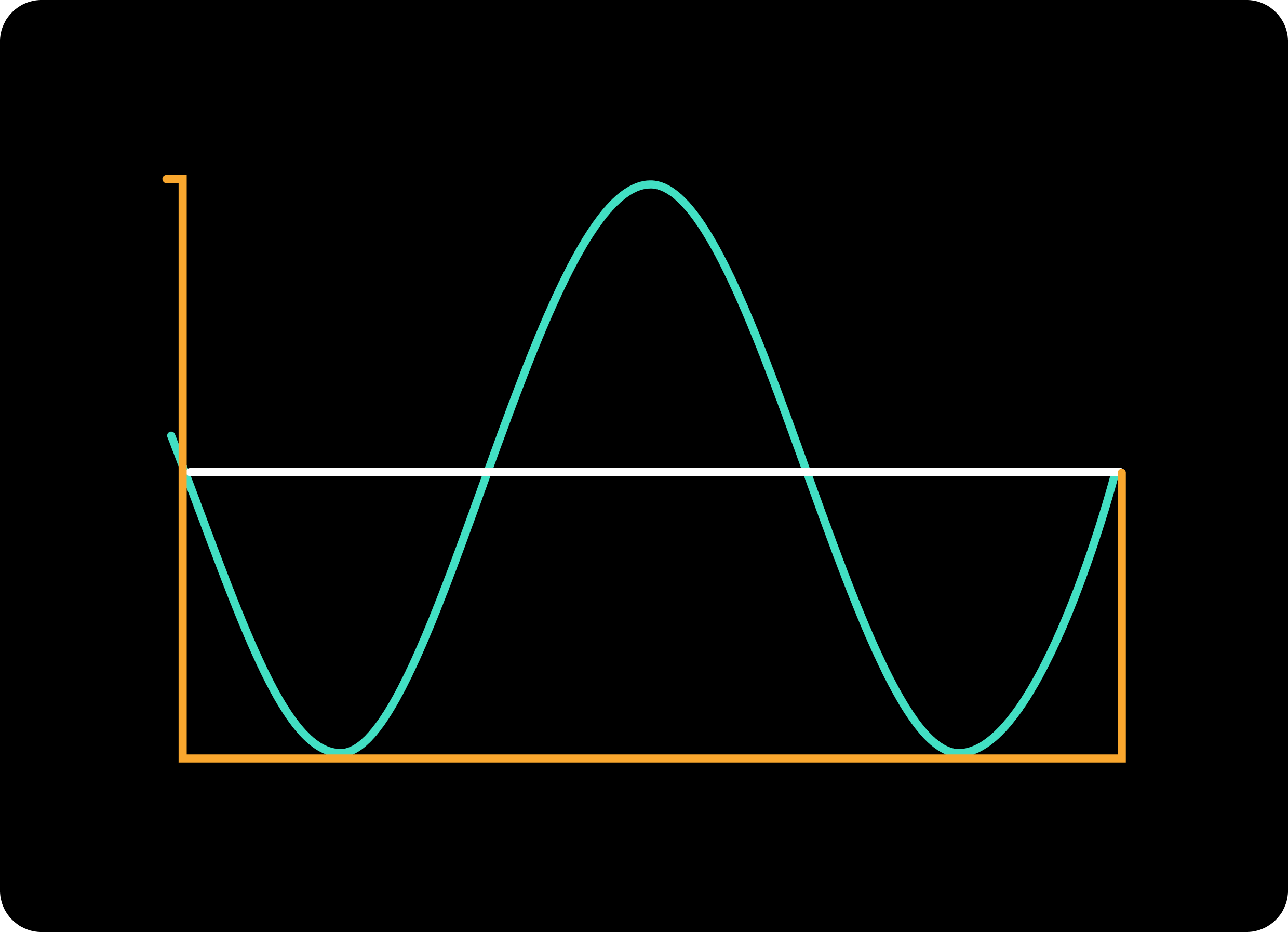
Both waves are negative on average. Wonderful!

That means, the sin wave (Cyan) is a component of the complex wave (Orange). See how easy it was to interpret using integrals!

---

Making this even easier

Instead of separating the waves into regions and inspecting the negativity/positivity region by region, we can have another math trick. What is this trick? It is multiplication!

Remember, what we want is: the signs of the waves to be the same (if one wave is negative in one region, the other one should be negative as well, same for the positive). Recall the property of multiplication below:

$$(+)(+) = (+) \newline (-)(-) = (+)$$

So, if we multiply the two regions’ integrals, and if the result is positive, that means the regions’ positivity/negativity is matching! Exactly what we wanted :)

You might have noticed, division would also work fine. We only care for detecting the same signs. I will go with multiplication for now because the illustrations will be simpler. But keep in mind that, division is also a valid candidate.

To demonstrate what multiplying two waves look like, here is $\sin(x)$:

And here is an example of multiplying $\sin(x)$ with itself. Images are generated from Wolfram Alpha.

Here is an important outcome, since $\sin(x)$ is correlated to itself (duh), we don’t have any negative values for $\sin^2(x)$. We multiplied those negative values with themselves and got positive values!

A quick summary of what we will do:

1. multiply two waves
2. take the integral of the multiplication
3. if the result is positive, these two waves are correlated!
4. No need to inspect region by region! Whole thing in a single equation!

How easy was that! Wow! Oh MY GOD!

You can watch a great video about this (the above images above are also copied from that video)

Recap: if we want to figure out if $\sin(3x)$ is a component of a wave of a complex function $f(x)$, then we can write:

$$\int f(x)\sin(3x)dx$$

And, if we want to generalize our function, we can introduce a Greek letter to scare people off. Let’s use omega: $\omega$

$$A(\omega) = \int f(x)\sin(\omega x)dx$$

Which translates to: if $A(\omega)$ is positive, it means $\sin(\omega x)$ is a part of our complex wave $f(x)$.

A Big Reminder

We do not know what’s inside $f(x)$. It is a black-box to us. We only know that the data points generated by $f(x)$. If we had known the internals of $f(x)$, we could have figured out the components of $f(x)$ without having to deal with all these. The goal here is to decrypt the complex wave denoted $f(x)$, which is a black-box.

In other words, $f(x)$ can be: $3\sin(5x) + \sin(2x)$, or $57\sin(7x) + 41\sin(3x)$, or any other complex wave. We don’t know. That’s what are going to discover using Fourier Transform.

Time for an example!

• complex wave: $f(x) = 3\sin(x) + \sin(2x)$ (we don’t know it yet)
• components of this complex wave are: sin(x) and sin(2x) (we don’t know it yet)
• If we apply this formula for our components:

  • we should get a positive value for analyzing frequency 1:

    $$A(1) = \int f(x)\sin(x)dx$$

  • we should get a positive value for analyzing frequency 2:

    $$A(2) = \int f(x)\sin(2x)dx$$

  • we will inspect other frequencies (3, 4, and so on…), but the result will be always 0, since our complex wave does not include other frequencies (for example, sin(3x) is not part of our complex wave).

Note that, the value for A(1) should be 3 times the value we get for A(2), because the amplitude of sin(x) is 3 in our complex wave, whereas the amplitude of sin(2x) is 1.

Let’s plug them in (but we can’t compute for infinity with calculators, so I will be merciful to calculators and compute only for 2π.

$$A(1) = \int_0^{2\pi} (3\sin(x) + \sin(2x))\sin(x) dx = 9.4248$$ $$A(2) = \int_0^{2\pi} (3\sin(x) + \sin(2x))\sin(2x) dx = 3.1416$$

Oh my… 9.4248 is exactly 3 times of 3.1416 !

And, lastly, an example for a wave that is not a component of the complex wave:

$$A(3) = \int_0^{2\pi} (3\sin(x) + \sin(2x))\sin(3x) dx = 0$$

$A(\omega)$ is just giving us the coefficients (amplitudes) of the related sine wave. Very useful…

Note before the next section: to increase readability, I might omit the dx from the integrals

OUTCOME:

1. Recall from the last section, waves are actually preserved when added together.
2. We can utilize multiplication or division to detect matching signs (positive or negative).
3. To see how much correspondence there is between the complex wave and the candidate wave, we can multiply the complex wave with the candidate wave.
4. If the result is positive, then it means, their frequencies match (since their positive/negative fields match).

5. And the magnitude of the result means, how much the frequencies match:

   $$A(\omega) = \int f(x)sin(\omega x)dx$$

---

Step 2: sinx is not enough

The problem with the below equation is:

$$A(\omega) = \int f(x)\sin(\omega x)$$

It cannot give us the phase of the sine wave. We can detect which sine wave is in the complex function f(x), and we can even detect the amplitude. But we cannot detect the sine wave if the phase is shifted. Here are some shifted sine waves:

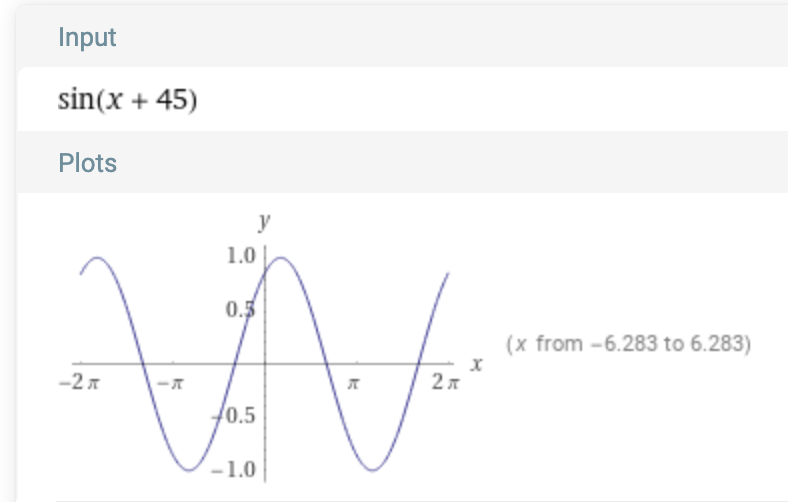
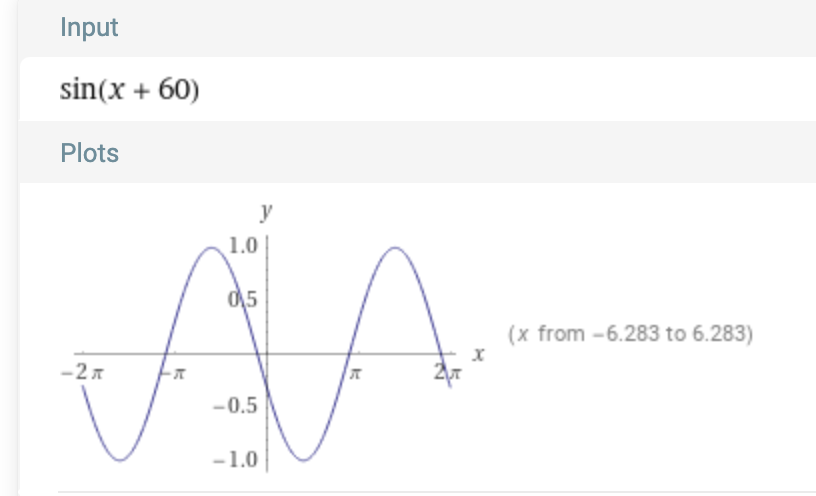
So, in short, if the complex wave f(x) includes something like sin(3x + 50), our formula won’t be able to extract that from the complex wave. Our function is only able to detect sin(ωx) as you can recall, not sin(ωx + a).

To be able to inspect all kinds of waves, pure sine is not enough on its own.

But, good news: sine and cosine are orthogonal to each other. Which means in basic English: with a combination of cosine and sine, we are able to form any periodic wave. It is possible to denote every periodic wave/function with:

$$f(x) = \int_{\omega=-\infty}^{\infty} A(\omega) \cos(\omega x) + B(\omega) \sin (\omega x)$$

Where A(ω) and B(ω) are the coefficients of the linear combination for the ωth basis vectors (the cos and sin).

The above equation translates into: if you add various cosine and sine waves together, with different coefficients, you can get any periodic function you like.

I’ll not dig any more deeply into the mathematics of how sine and cosine are orthogonal to each other, and why using both of them grants us the ability to form any periodic function. Answering these questions will be diverging from Fourier Transform at this point.

You probably see where I’m arriving at: using both sine and cosine in our equation will allow us to extract the phase information. How? We will see below.

Since sine and cosine are both basis vectors, we could as well have used cosine till now instead of sine, and every intuition we had so far would be the same. But as sine is not enough on its own, cosine is not enough either.

Recall the equation:

$$f(x) = \int_{\omega=-\infty}^{\infty} A(\omega) \cos(\omega x) + B(\omega) \sin (\omega x)$$

which can also be written as:

$$f(x) = \int_{\omega=-\infty}^{\infty} A(\omega) \cos(\omega x) + \int_{\omega=-\infty}^{\infty} B(\omega) \sin (\omega x)$$

Now, it should be clear: if we compute two different versions of our formula with sine and cosine, we should be able to extract every piece of information from the complex function f(x).

$$A(\omega) = \int f(x) \sin(\omega x)$$ $$B(\omega) = \int f(x) \cos(\omega x)$$

Because, f(x) is nothing but a combination of various cosx and sinx in the end.

OUTCOME:

1. All complex waves are some combination of sine and cosine waves in the end.

2. We need to inspect our complex wave for both sine and cosine waves to be able to fully inspect it:

   $$A(\omega) = \int f(x) \sin(\omega x)$$ $$B(\omega) = \int f(x) \cos(\omega x)$$

---

Step 3: e^i

In the previous step, we ended up having 2 formulas (one for sine, one for cosine). Thanks to math, there is a more compact way.

There is this thing called Euler's formula:

$$e^{i\phi} = \cos\phi + i\sin\phi \newline e^{-i\phi} = \cos\phi - i\sin\phi$$

Again, the intuition behind why Euler's Formula holds is a different topic than Fourier’s Transform. And it is not a blocker for understanding Fourier Transform. So I won’t be explaining that. But in case you are like me, here are two great resources that fulfilled my curiosity:

• Euler’s formula with introductory group theory

• [What is Euler’s formula actually saying?

  Ep. 4 Lockdown live math](https://www.youtube.com/watch?v=ZxYOEwM6Wbk)

---

Why is there an imaginary number i here in the formula?!

Remember, i is for imaginary, and when you multiply a number with i, you basically transfer that number to the imaginary realm (a new dimension).

In short, i is granting us a new dimension, turning our function from being 1 dimensional to 2 dimensional. This way, our cosx and sinx do not collide with each other, and we can inspect both of them in a single formula! Actually, the intuition behind i was that simple. No need to be scared at all.

There are other great perspectives about i; for example, watch from the timestamp (warning: you might get confused): But what is the Fourier Transform? A visual introduction.

The most upvoted answer to a question I asked on reddit, provided another great take on cosx + isinx. So I will directly share it here (shoutout to zarek911 for his amazing answer):

Reddit answer begins

By using cosωx and sinωx alone, we have 2 different “types” of basis vectors in the same basis and for that reason we need to have 2 different component functions A(ω) and B(ω). To simplify this we can change the basis into the set of cosωx + isinωx and cosωx - isinωx, still for all ω from 0 to infinity. Conveniently these can be expressed using Euler’s formula, the first being:

$$e^{iwx}$$

and the second being:

$$e^{-iwx}$$

And this is no information lost from our cos and sin basis since you can always recover them with:

$$\cos(wx) = \frac{(e^{iwx} + e^{-iwx})}{2}$$

and

$$\sin(wx) = \frac{(e^{iwx} - e^{-iwx})}{2i}$$

So at first, it seems like you still have 2 types of basis vectors and you still need 2 different component functions, but you can see that the 2nd type of basis vector:

$$e^{-iwx}$$

is just the first:

$$e^{iwx}$$

with a negative value of ω. So you can actually combine these 2 different types into one type by letting ω run from $-\infty$ to $\infty$. So now the linear combination would have a single component function A(ω) and would look like:

$$f(x) = \int_{-\infty}^{\infty} A(\omega) e^{i\omega x}$$

Reddit answer ends

OUTCOME:

1. We need to inspect both sine and cosine, and hence we needed two formulas:

   $$A(\omega) = \int f(x)\sin(\omega x)$$ $$B(\omega) = \int f(x)\cos(\omega x)$$

2. By introducing another dimension with i, we can now use sine and cosine in the same formula:

   $$f(x) = \int_{-\infty}^{\infty} A(\omega) \cos\omega + i\sin\omega$$

3. Which is equal to:

   $$f(x) = \int_{-\infty}^{\infty} A(\omega) e^{i\omega x}$$

---

Step 4: why is there a - in the original formula instead of +?

In the original formula:

$$A(\omega) = \int_{-\infty}^{+\infty} f(x)e^{-i\omega x}dx$$

there is a - sign in the exponent as you can see. And if we remember Euler's Formula:

$$e^{i\phi} = \cos\phi + i\sin\phi \newline e^{-i\phi} = \cos\phi - i\sin\phi$$

then, we know that our original formula for Fourier Transform actually corresponds to:

$$A(\omega) = \int_{-\infty}^{+\infty} f(x)(\cos(\omega x) -i\sin(\omega x))dx$$

But wait… Previously, we used cosx + isinx to represent both cosx and sinx in the same formula. So, how did this + turn into a -?

Here is where everything will come together and make even more sense. Let’s go back a bit and have a quick recap. It will be helpful.

Constructing any function from sine and cosine:

$$f(x) = \int_{-\infty}^{\infty} A(\omega) \cos\omega x + B(\omega) \sin \omega x$$

We can also approach the same thing from the perspective that zarek911 provided (merging cosx and sinx using an additional dimension with i, so that they won’t overlap):

$$f(x) = \int_{-\infty}^{\infty} A(\omega) (\cos\omega x +i\sin \omega x )$$

If we try to explain the above formula in basic English, it would go like this (very roughly):

Multiply some frequencies with cosx and sinx, and sum intermediate results to form a complex wave.

The above formula is also equal to:

$$f(x) = \int_{-\infty}^{\infty} A(\omega) e^{i\omega x}$$

Did you notice something? We are doing the opposite of Fourier Transform. We are composing a complex wave from basic waves. Fourier Transform decomposes a complex wave into basic waves, and inverse Fourier Transform composes waves into a complex one. We just figured out the inverse Fourier Transform!

Although the name implies that Fourier Transform is more intuitive than inverse Fourier Transform, I believe it is not the case. Making a cocktail is simpler to understand than figuring out the ingredients of a cocktail.

Alright! We just need to inverse the inverse Fourier Transform then… And we should have a normal Fourier Transform. Let’s go! And it will be very easy actually.

Here is a great analogy I’m stealing from here:

Say, you have 5$ banknotes, and someone asks you to put 3 of them together. Now you have, 3x5=15$ as a pile.

In this analogy:

• let 5$ banknotes, be: cosωt + isinωt (the base components)
• 3 times, be: A(ω) (the amplitudes / amount)
• 15$, be: f(x) (the complex wave)

What we have done is inverse Fourier Transform. To compose waves, we are multiplying waves and coefficients (amplitudes) together.

Referring to the primitive version of our formula again:

$$f(x) = \int_{-\infty}^{\infty} A(\omega) \cos\omega x + B(\omega) \sin \omega x$$

We multiplied A(ω) (amplitude) with cosωx (wave), and we summed up these multiplications (the same goes for sine).

To decompose waves, we will divide the complex wave by basic waves and get the amplitudes (coefficients).

Say, there is a pile of 15$ dollars, and you need to figure out how many 5$ banknotes are there potentially. What would you do? You divide 15 by 5, and get 3 as a result.

Recall, when we were figuring out the first versions of our formula:

$$A(\omega) = \int f(x)\sin(\omega x)dx$$

we multiplied f(x) by sin(x), because we needed the signs to be the same. And I mentioned back then, division would have worked just fine. Now, if you think of Fourier Transform (we are decomposing waves), and connect the pieces with the analogy I provided above, division makes a lot more sense than multiplication. So:

$$A(\omega) = \int \frac{f(x)}{\sin(\omega x)}dx$$

Yeah. This formula would also do.

So, why did I provide you the multiplication version in the beginning? Why did I bother explaining multiplication is also working?

Because, the important part was to detect if the signs were matching amongst two different waves. It was NOT that “division works because it makes sense to divide the complex function by the basic waves”. If that was the case, multiplication wouldn’t work.

Imagine this:

• I just gave you the 5$ banknote analogy in the beginning, without explaining that sign stuff.
• And we did not spend time for understanding how waves work.
• And then you try to explain Fourier Transform to someone.
• You went with “for decomposing waves, you need to DIVIDE the complex wave by the basic waves because it makes sense according to the 5$ banknotes analogy”
• and they said: “well, I tried multiplying a sine wave with the complex function, and I was able to extract the sine waves out of the complex function… I think your analogy is a bit off, eh?”

• so, it would be like this:

  

• I didn’t want you to become an alcoholic. That’s why I provided you with the detail of matching signs of two different waves, and we dove into the basics of waves work.
• The division/multiplication 5$ banknotes analogy is good for understanding Fourier Transform and inverse Fourier Transform in comparison. But it is not that accurate for understanding Fourier Transform on its own in my opinion.

again, take a look at our latest formula for inverse Fourier Transform:

$$f(x) = \int_{-\infty}^{\infty} A(\omega) e^{i\omega x}$$

we are multiplying the amplitudes A(ω), with basic waves e^iωt. Now, we got to divide the complex wave f(x) with our basic waves e^iωt.

$$A(\omega) = \int_{-\infty}^{\infty} \frac{f(x)}{e^{i\omega x}}dx$$

this is equal to:

$$A(\omega) = \int_{-\infty}^{\infty} f(x)e^{-i\omega x}dx$$

and of course, this is equal to:

$$A(\omega) = \int_{-\infty}^{\infty} f(x)(\cos(\omega x) - i\sin(\omega x))dx$$

There you go… Here is your - instead of + :)

We’ve done it! That was it for the Fourier Transform.

OUTCOME:

1. To be able to know how much of a candidate wave there is inside complex wave, we have to divide complex by candidate:

   $$A(\omega) = \int_{-\infty}^{\infty} \frac{f(x)}{e^{i\omega x}}dx$$

2. Which is equal to:

   $$A(\omega) = \int_{-\infty}^{\infty} f(x)e^{-i\omega x}dx$$

---

Recap (and a bonus)

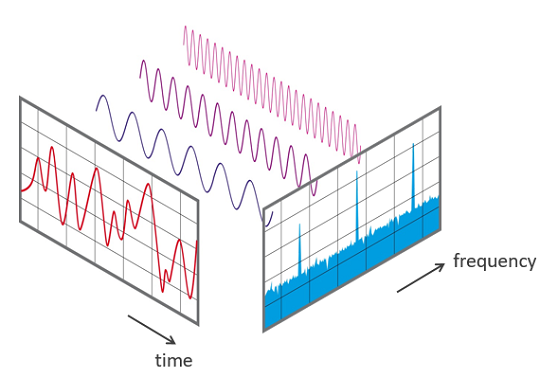image taken from: NTI Audio

Remember from this image, Fourier transform is going from the time-domain to the frequency-domain. Let’s change the letters in our notation accordingly, so that it will make more sense.

This:

$$A(\omega) = \int_{-\infty}^{\infty} f(x)e^{-i\omega x}dx$$

is now this:

$$\hat{g}(f) = \int_{-\infty}^{\infty} g(t)e^{-ift}dt$$

The changes:

• x → t (since we are representing time with this letter)
• ω → f (since we are representing frequency with this letter)
• f → g (since now, we have another f (frequency), so let’s change this)
• A → ĝ (to make it related to the new g)

The formula is still the same, the intuitions are the same. We just changed letters :)

---

The bonus

We could also add 2π to our formula. Why? Because of three reasons:

1. It will make the math part more convenient, but we are not interested in that kind of math in this post. We only care for the intuitions.

2. As humans, we like the most basic things to be equal to 1. So, the most basic period should be 1. How do we achieve 1 with cosine and sine? With 2π of course! Let’s see the differences between sinx and sinπx below from Wolfram Alpha:

   

   

3. If you have watched 3b1b’s video that I gave the link above (I’ll not give the link again, go find it), this also makes more sense for winding the wave around a circle.

Basically, we have three good reasons to do this, and not a good one against it as far as I know. So, let’s do it!

Ladies and gentlemen, I present you the final form of our Fourier Transform!

$$\hat{g}(f) = \int_{-\infty}^{\infty} g(t)e^{-i2\pi ft}dt$$

We’ve done it! That was it for the Fourier Transform. Fortunately (or unfortunately) we still have more to do. First, we need to come up with a discrete version of the Fourier Transform.

But for simplicity, I will use the version without 2π. We will see in the next part, there are even better arguments to include 2π when we are dealing with both DFT and FFT.

OUTCOME:

1. Introducing 2π to our formula is another small addition (yet not that important):

   $$A(\omega) = \int_{-\infty}^{\infty} f(x)e^{-i2\pi\omega x}dx$$

2. To have more meaningful letters and to follow the convention, we can also denote our formula as:

   $$\hat{g}(f) = \int_{-\infty}^{\infty} g(t)e^{-i2\pi ft}dt$$

---

What is Discrete Fourier Transform (DFT)?

In the real world, electronic sensors do not capture values continuously. What I mean is, they have precision. For example, a sensor’s precision could be milliseconds, so it is recording data for each millisecond. This means, our data at hand is discrete, not continuous. We cannot zoom in indefinitely; there is a precision limit.

Discrete Fourier Transform is the same as Fourier Transform but allows us to compute the same stuff on discrete data instead of continuous data (for example, using summation of data points instead of taking the integral of a continuous function).

It’s much more realistic. We want to analyze a complex wave function. We only have some data points that these complex wave generated. We will input these data points to DFT, and it will output the ingredients of the complex function.

So, how do we turn our continuous function into a discrete one?

First, we turn our integral into a sum. The integral is the continuous form of the $\sum$ symbol. One adds all points, the other one adds discrete points.

$$\hat{g}(f) = \int_{-\infty}^{\infty} g(t)e^{-ift}dt$$

will turn into:

$$\hat{g}(f) = \sum_{t = -\infty}^{\infty} g(t)e^{-ift}$$

But, the ranges do not make sense now. We don’t have infinities in discrete form (or in real life). We will have a finite point of data to evaluate. So, our range will be, from the first point, till the last point. Let n denote a point, and let N be the total amount of data points we have.

$$\hat{g}(f) = \sum_{n=1}^{N} g(t)e^{-ift}$$

Previously, we were interpreting f (frequency) and t (time) continuously. Well, guess what, we can’t now.

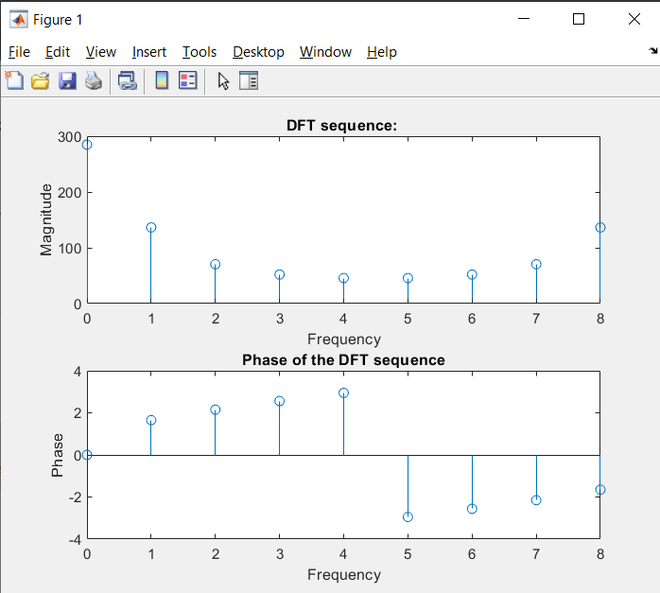image taken from: geeksforgeeks

This image represents the output of DFT. Just like FFT, we have 2 outputs:

• Real part (frequency-magnitude values)
• Imaginary part (phase-magnitude values)

In the frequency-magnitude plot, we have 9 discrete points (0,1,2,3,4,5,6,7,8) for frequency in this example. The letter k will denote these points. Be careful not to confuse k and n.

• k is the frequency we are trying to find out (for example, say there is sin2x as a component. 2 here is the k).
• n is the data point we have available for the function we are analyzing.
• Both n and k are bounded by N (the total amount of data points).
• n is bounded by N because n is the data point, and we have N data points in total (duh).
• k is also bounded by N because we cannot inspect a frequency that is bigger than the amount of our data points. There is a theorem about this that I will not go into details of (Nyquist–Shannon sampling theorem), but if you are familiar with polynomials, this should make sense. N+1 points required to specify an N degree polynomial.

Simply, f (continuous frequency) becomes k (discrete frequency). Nothing much is happening here, just a change of letter. We could have kept the old letter, but let’s just follow the convention. When we use f, we should understand a continuous frequency; whereas when we use k, we should understand a frequency bin (as presented in the above image).

$$\hat{g}(k) = \sum_{n=1}^{N} g(t)e^{-ikt}$$

We cannot represent t (all the points possible, or time) in a discrete setting. Instead of infinite points, we have finite points (which are denoted by n).

We need to be compact, and select the minimum amount of points, and use these points in our formula.

Recall our basis vectors (sine and cosine). Their period is 2π. And we have N points in total. So, dividing 2π into N points would make the most sense for evaluating our sine and cosine functions (previously, we were evaluating them at all points).

$$\hat{g}(k) = \sum_{n=1}^{N} g_ne^{-ikn2\pi/N}$$

Notice that we actually also changed g(t) into g(n2π/N). But to be compact, we denoted it with the nth element of the series g. So, we are consistent :)

Well, there you go:

OUTCOME:

1. We had this:

   $$\hat{g}(f) = \int_{-\infty}^{\infty} g(t)e^{-ift}dt$$

2. We turned the integral into a sum:

   $$\hat{g}(f) = \int_{-\infty}^{\infty} g(t)e^{-ift}dt$$

3. We turned infinite bounds into finite bounds:

   $$\hat{g}(f) = \sum_{n=1}^{N} g(t)e^{-ift}$$

4. Changed the letter f to k to denote discrete frequency:

   $$\hat{g}(k) = \sum_{n=1}^{N} g(t)e^{-ikt}$$

5. We can’t have continuous time. So, changed t to 2π/N (where 2π is the frequency period, and N is the total amount of data points, effectively becoming points in time):

   $$\hat{g}(k) = \sum_{n=1}^{N} g(2\pi/N)e^{-ikn2\pi/N}$$

6. Denoted g(n2π/N) more compactly (due to convention) as nth element of series g:

   $$\hat{g}(k) = \sum_{n=1}^{N} g_ne^{-ikn2\pi/N}$$

---

A Small Warning About the Internet

When it comes to math, especially in the form of a video about math, people tend to take it as a fact.

We are taught not to believe everything we see on the internet. However, the scope of skepticism is often narrowed down to not trusting comments and social content. Scientific papers or videos, on the other hand, are often unquestionably accepted.

In this video, it is explained:

• f → k/N
• n → t

In the comments, people express their gratitude towards the individual who created the video.

However, I’ve spent many hours trying to understand the reasons for these replacements:

• f → k/N
• n → t

This explanation also contradicted some of the approaches presented in other resources (for example: Oxford Robotics - Signal Processing Lecture 7).

In short, this video caused me to lose many hours, especially as a newbie to the concept. Fortunately, I questioned this part along with every other thing he said.

I believe most of the audience in this video simply accepted the above replacement as a fact. If I were to ask them:

• why f → k/N?
• and why we only replaced f with k/N in the exponent, but not in the X(f) part?

They probably wouldn’t have a good answer. They did not grasp the intuition; they merely memorized it. I, too, fell into this trap when I first saw this video.

So, even for me, it was easy to be lazy and succumb to this trap. I believe this is a great example of why you should question even the scientific information you encounter on the internet.

Now that I’ve fulfilled my social duty as well, let’s go back to the Fourier Transform!