---

What is it good for?

Compared to Merkle tree proofs, the proof size is constant.

In the end of this article, we will be able to replace Merkle proofs with KZG polynomial commitments, and our proof will always be constant (48 bytes), regardless of the array size or the polynomial order.

---

Polynomial commitments via Merkle trees

Recap on polynomials (skip this if you are already familiar with them)

A polynomial is nothing but adding some powers of $x$, combined with some coefficients. It is demonstrated via: $p(X)$. The tradition is, capital letters are for abstract polynomial, for example $p(X)$, in this one, $X$ can be anything, it could be the secret key, it could be a random data point, it can be anything. Whereas small letters are for certain values, for example $p(s)$, in this one, $s$ will be a certain value (the secret key).

Some examples:

The polynomial $p(X)$ can be anything. For example: $p(x) = 5x^3 + (1)x^2 + 7x^1 + 6(x^0)$, which can be also expressed as:

$$5x^3 + x^2 + 7x + 6$$

or $p(X)$ can be: $6x^5 + 0x^4 + 0x^3 + 0x^2 + 0x^1 -55x^0$, which can be also expressed as:

$$6x^5 - 55$$

notice that, even in $6x^5 - 55$, there are actually 6 coefficients (0’s are omitted for brevity) → 6, 0, 0, 0, 0, -55

Recap on polynomials (end)

The relationship between data and polynomials:

It is enough to have only coefficients to construct a polynomial. We can treat our data points as coefficients, allowing us to construct a polynomial for our data.

If our data is 6, 0, 0, 0, 0, -55 → then the polynomial will be $6x^5 + 0x^4 + 0x^3 + 0x^2 + 0x^1 -55x^0$, or for the shorter version: $6x^5 - 55$. There is exactly one and only one polynomial for a specific coefficient set. In other words, there is one-to-one mapping between polynomials and coefficients.

Have some math culture! Mmmhh, delicious:

the formal definition is:

$$p(X) =\sum_{i=0}^{n}c_ix^i$$

where $c_i$’s are the coefficients. For the ones who don’t like math, this mambo-jambo basically means:

• multiply the coefficients $c_i$ with $x^i$ (powers of $x$)
• then add them all together

in the end, we will have a polynomial with a degree of $n$ (means, the highest power of $x$ will be $n$)

What are polynomial commitments?

This means, we will commit to some polynomial $p(X)$, and then we will claim that at the point $z$, this very polynomial will give the result $y$. In math language, $p(z) = y$.

The verifier will request a proof that we did not change the polynomial in order to make $p(z) = y$. In other words, the verifier wants to be sure about the equation $p(z) = y$ will hold for the very polynomial that is selected in the beginning.

To provide a proof to the verifier, we can commit to the polynomial selected in the beginning. How? By calculating the merkle root of the coefficients.

Introduction to merkle trees

---

An Example Run of Constructing a Polynomial Commitment using Merkle Trees

Say our $p(X) = 5x^3 + (1)x^2 + 0x^1 + 6(x^0) = 5x^3 + x^2 + 6$

The coefficients are: 5, 1, 0, 6

Now, we will build a Merkle tree out of these coefficients.

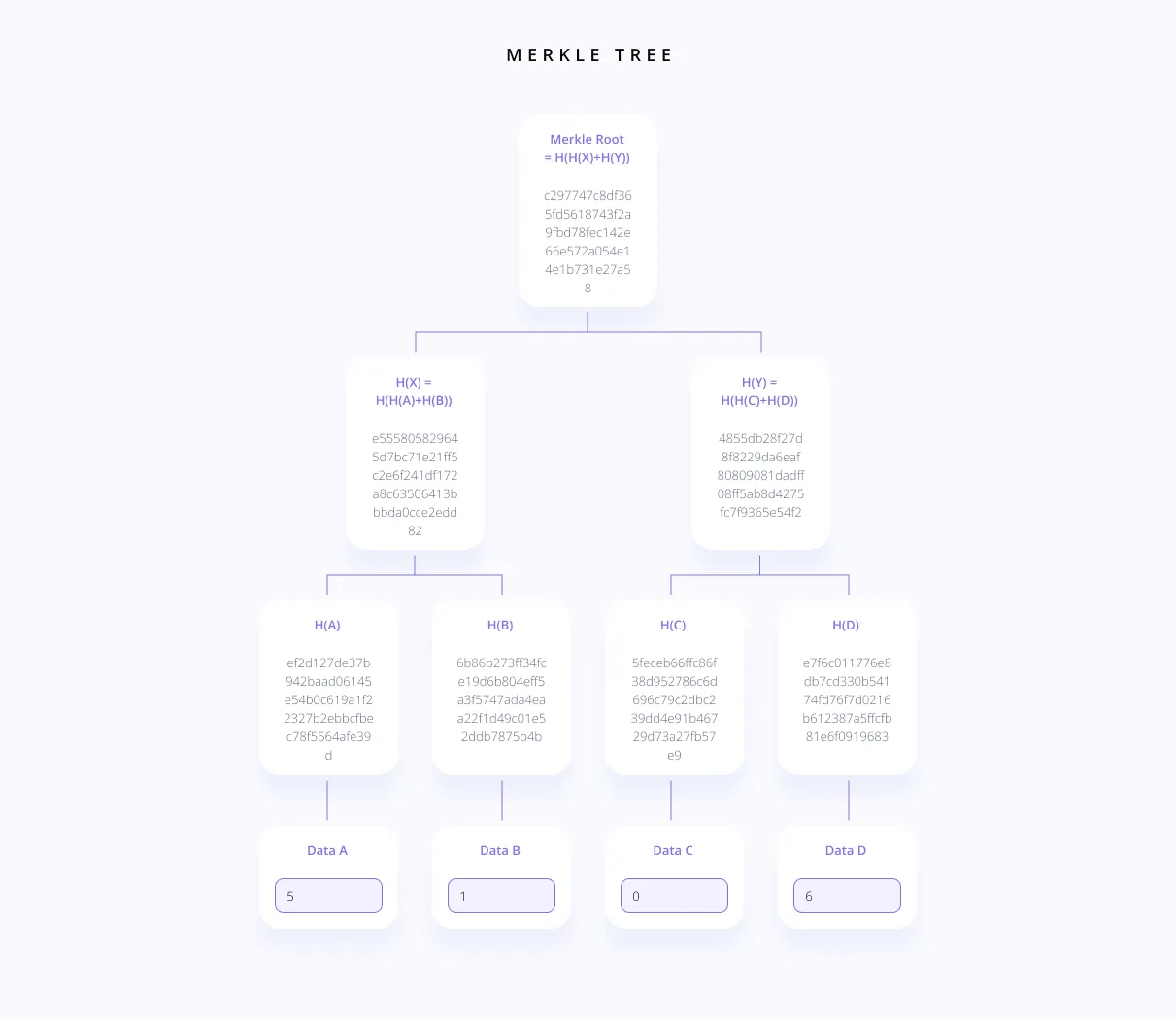I used this link to generate this image: https://blockchain-academy.hs-mittweida.de/merkle-tree/

As the first thing, we will send our commitment (the Merkle root) to the verifier. Then the verifier will give us a value (say, it will be $2$), and ask for the evaluation for this value for our polynomial. Note that, the verifier does not know the polynomial yet.

Now, say we are the prover, and our claim is $p(2) = 50$ , which is correct (we choose not to cheat). But there can be multiple polynomial that can hold the above equation, for example:

$$p'(X) = 25x$$

We should prove that the equation $p(2) = 50$ holds for the original polynomial, which is:

$$p(X) = 5x^3 + x^2 + 6.$$

To prove this, we can send all the coefficients to the verifier 5, 1, 0, 6 and the Merkle root: c297747c8df365fd5618743f2a9fbd78fec142e66e572a054e14e1b731e27a58

The verifier will check for 2 things:

• given the polynomial coefficients, she will construct the polynomial, and compute the result herself, and check if our claimed result is matching with what she computed → $p(2) \stackrel{?}{=} 50$. If they are matching, good :) If the computed results are not matching, that means someone in this protocol is retarded.
• if the first check holds, then she will construct the Merkle tree for these coefficients herself, and compare our Merkle root provided in the proof, with her Merkle root (which she computed herself). If they are matching, that means we did not change the polynomial!

Why the Merkle root is enough to prove that we did not change the polynomial?

Because: hash functions are not reversible. If we found another polynomial, for which the equation is true → $p'(X) = 25x$, then we have to send the coefficients of this polynomial to the verifier, and generate a Merkle tree from the coefficients for this polynomial. Recall that we already sent a Merkle root to the verifier as the first step of the protocol, and generating a fake polynomial for which the Merkle root will be equal to the one we sent to the verifier, is practically impossible.

Summary of the protocol:

1. prover has a polynomial, he commits to it, and sends to the commitment to the verifier
2. verifier has a value, sends this to the prover, and asks for an evaluation for this value
3. prover evaluates the value, sends the result, and sends the coefficients of the polynomial
4. verifier constructs the polynomial herself:
   • computes the result for the value, checks if the prover’s evaluation is the same
   • constructs the merkle tree for the coefficients, checks if the prover’s merkle root is the same

Let’s overview the properties of this scheme:

• the commitment was a single element, which is the Merkle root (typically 32 bytes)
• the prover had to send all the coefficients
  • the whole polynomial is shared with the verifier, nothing is secret in this scheme
  • the data need to be send to verifier is linear: if our polynomial had 1.000.000 coefficients, then we will send 1.000.000 coefficients… In other words, the proof grows as the polynomial grows, this is not very scalable
• the verifier had to reconstruct the polynomial, re-calculate the whole computation
• verifier had to reconstruct the whole Merkle tree

Committing to a polynomial via Merkle trees did not make much sense? Great! Because it… doesn’t… It is silly and inefficient. But it will help us understand what polynomial commitments are, and then we will significantly improve it using Kate Proofs.

What we will achieve with Kate scheme:

• commitment size will be 48 bytes (yeah, 12 bytes larger than before)
• The proof size, independent from the size of the polynomial, is always only one group element. Verification, independent from the size of the polynomial, requires two group multiplications and two pairings, no matter what the degree of the polynomial is. This means, the proof size is constant! UNBELIEVABLE!
• The scheme hides the polynomial (practically: yes; theoretically: not 100%, if the polynomial is very simple, it can be guessed. But it shouldn’t be simple in the first place)

The promises are amazing! Let’s learn how it works.

---

Combining Elliptic Curves and Secure Multi-Party Computation

In cryptography, we have access to a powerful tool, called secure multi party computation (MPC). It basically allows us to collectively generate a secret (let’s denote this with $s$). But in the end (here is the good part), no-one will know the secret!

In order to reveal $s$, all the participants would have to collude (they cannot reveal the secret even if all of them are compromised, except one. EVERYONE needs to be corrupted).

Now, the best part is coming: without knowing the value of this secret number $s$ (that is why, it is secret), we can actually compute $p(s)$ in elliptic curve setting.

How? Well, if you are unfamiliar with basic elliptic curve cryptography, you might need to read the first the parts of this series.

Let $\mathbb{G}$ be the points on our elliptic curve, and $G$ be the generator of $\mathbb{G}$.

A generator is a point on elliptic curve, a base point, which, when added to itself generates all other points on the curve. A simple analogy would be 1 for integers: 1+1 = 2, 1+1+1 = 3, and so on, you can get any integer by adding 1 to itself enough times.

Then, $\left[ x \right]$ is defined as:

$$\left[ x \right] = xG = \underbrace{G+...+G}_{\text{x times}}$$

In other words, $\left[ x \right]$ means, $x$ is converted to a point in the elliptic curve (it will correspond to one of the points in $\mathbb{G}$).

A good property of elliptic curves is you cannot derive the value of $x$ from $\left[ x \right]$. After multiplying $x$ with $G$, the value of $x$ is now hidden. You cannot simply divide $\left[ x \right]$ with $G$, if you are wondering why, it means you didn’t read the link for ECC (Elliptic Curve Cryptography) up there. Checkmate :)

So, the first thing we will do in our scheme, is to generate a secret number $s$, and then compute

$$\left[ s^0 \right], \left[ s^1 \right], \left[ s^2 \right], ... , \left[ s^n \right],$$

(where $n$ is the order(degree) of our polynomial), in an MPC setting. These computed values will be public knowledge, everyone will have access to them. But remember, it is impossible to deduce $s$ from these, and also, it is impossible to compute another power of $s$ from these: we cannot compute $\left[ s^{n+k} \right]$).

What we can do with these computed values instead, is:

• we can multiply those with a coefficient. Multiplying $s$ with $G$ will allow us to hide $s$ (thanks to elliptic curves)

$$c\left[ s^i \right] = cs^iG = \left[ cs^i \right].$$

• that means, we can actually compute $\left[p(s)\right]$.
  • by basically multiplying every coefficient $c_i$ with $\left[ s^i \right]$
  • going back to one of our examples, our coefficients were: $6,0,0,0,0,-55$
  • so we should compute $6\left[ s^5\right] + 0\left[s^4\right] + 0\left[s^3\right] + 0\left[s^2\right] + 0\left[s^1\right] - 55\left[s^0\right]$

  • the whole thing can be shown with:

    $$\left[ p(s)\right] = \left[ \sum_{i=0}^n c_i s^i \right] = \sum_{i=0}^n c_i \left[ s^i \right]$$

This means, we just computed the elliptic curve point equivalent of $p(s)$, (which is $\left[ p(s) \right]$ ), without knowing the secret value $s$.

---

Kate Commitment

Pronounced kah-tey

In KZG polynomial commitment scheme, the prover first needs to commit to the polynomial $p(X)$ (this polynomial will be generated from our data points, for example, our data points can be the coefficients of this polynomial), and then submit a proof $\pi$ , along with his claim $p(z) = y$. I’ll explain what that all means soon, we will proceed step-by-step.

The point $z$ will be selected by the verifier, and sent to the prover after the prover sends his commitment $C = \left[ p(s) \right]$, which is a commitment to the polynomial $p(X)$.

The things that prover needs to know/compute:

• $C = \left[ p(s) \right]$ → The prover knows the polynomial $p(X)$, and we showed above how $\left[ p(s) \right]$ can be computed via an MPC setting.
• $p(z) = y$ → $z$ is provided to the prover from the verifier. The prover knows the polynomial itself, this is trivial.
• $\pi$, the proof → we haven’t talked about it yet. Let’s begin!

Now, the proof is another polynomial, which will help us to construct a relationship with the original polynomial $p(x)$. This will become handy when we want to prove we did not change the original polynomial as the prover. Because remember, we are not using Merkle proofs, and we need a way to prove that we did not change the original polynomial.

And it is time for some polynomial math!

If a polynomial $p(X)$ has a zero at point $m$, that means the polynomial $p(X)$ is divisible by the term $X - m$. Being divisible by the term $X - m$ means we can write the following:

$$p(X) = (X-m)q(X)$$

for some other polynomial $q(X)$. And this equation is clearly evaluates to zero at the point $X = m$.

An example:

1. $p(X) = 3x^2 - 5x - 2$ (let this be our polynomial)
2. $p(2) = 3(2^2) - 5(2) - 2 = 0$ (and we find a number that makes our polynomial evaluate to 0)
3. $$p(X) = 3x^2 - 5x - 2 = (X - 2)q(X)$$
4. $$\frac{3x^2 - 5x - 2}{x - 2} = q(X)$$
5. $$q(X) = 3x+1$$

If you are confused on step 4 and 5, we can divide polynomials using 2 different methods, one of them is by simple division (1), the other one is by factorization (2).

Coming to the crucial part:

1. we want to prove $p(z) = y$
2. we know $p(X) - y$ will be zero at the point $X=z$
3. in other words, we know $X - z$ divides $p(X) - y$

4. what we have is:

   $$\frac{p(X) - y}{X - z} = q(X)$$
5. we can compute the polynomial $q(X)$ now (as shown above).
   1. $X$ can be anything, so let it be $s$

   2. we now have the following relationship:

      $$\frac{p(s) - y}{s - z} = q(s)$$
   3. or another way to display this relationship: $p(s) - y = q(s)(s-z)$

We cannot work directly with this relationship, because both the prover and the verifier does not know $s.$ What do they know is, $\left[ s^i \right]$.

This relationship itself can be the thing that will convince the verifier. Why? Let’s see (skip this part if you are not interested in the proof):

• we already committed to $p(X)$ via $C = \left[ p(s) \right]$, this commitment is ensuring we cannot change $p(X)$. Reason:
  • Let’s assume otherwise. Say for another polynomial $p'(X) \neq p(X)$, we arrive at the same commitment, which means $\left[ p'(s) \right] = \left[ p(s) \right]$. And that means $p'(s) - p(s) = 0$. Then, we will be able to cheat by changing $p(X)$ with $p'(X)$. Now, we should prove that finding $p'(X)$ should be practically impossible.
  • For two different polynomials, we can write the following: $r(X) = p(X) - p'(X)$.
  • We know $r(X)$ is not a constant polynomial in this case (a.k.a. it’s order is not 0). How? Because if $r(X)$ were to be a constant polynomial, that would have meant the only difference between $p(X)$ and $p'(X)$ is the constant term. So something like below: $p(X) = ax^i + bx^j + cx^k + m$ $q(X) = ax^i + bx^j + cx^k + n$ notice that, between $p(X)$ and $p'(X)$, the only difference can be $m$ and $n$, and it should be $m \neq n$ in order to $r(X)$ to be a constant polynomial.
  • But, in that case, we cannot have $p'(s) - p(s) = 0$. It is a contradiction.
  • so, $r(X)$ is a non-constant polynomial (has some terms in it with $x$ in it).
  • Polynomial math fact: any non-constant polynomial of degree $n$ can evaluate to zero at most $n$ different points.
  • Recall the prover does not know the secret value $s$.
  • So, in order to have $p'(s) - p(s) = 0$, the prover’s best shot is to make $p(X) - p'(X) = 0$ in as many places as possible.
  • Since $r(X) = p(X) - p'(X)$, and say order of $r(X)$ is $n$. The prover can make $p(X) - p'(X) = 0$ in at most $n$ points.
  • recall: $\left[ p(s)\right] = \left[ \sum_{i=0}^n c_i s^i \right] = \sum_{i=0}^n c_i \left[ s^i \right] = \sum_{i=0}^n c_i s^i G = G\sum_{i=0}^n c_i s^i$
  • which means, this whole thing will ultimately evaluate to a point in the elliptic curve we selected
  • recall: $\left[ p'(s)\right] = \left[ \sum_{i=0}^n c'_i s^i \right] = \sum_{i=0}^n c'_i \left[ s^i \right] = \sum_{i=0}^n c'_i s^i G = G\sum_{i=0}^n c'_i s^i$
  • which again means, this whole thing will ultimately evaluate to a point in the elliptic curve we selected.
  • To make $\left[ p'(s)\right] = \left[ p(s)\right]$, means the generated points on the elliptic curve should be equal.
  • Some of the setup parameters are → $n = 2^{28}$ for the polynomial order, and $p \approx 2^{256}$ for the curve order (curve order means, the point amount on the curve).
  • Recall the prover’s best shot is to make $p(X) - p'(X) = 0$ in as many places as possible (which is $n$ points).
  • So the attacker would have $2^{28}$ possibilities in his hand to cheat.
  • But the possibility of having the same point on the elliptic curve for $\left[ p'(s)\right] = \left[ p(s)\right]$ for a single trial, is around $1/2^{256}$.
  • Ultimately, the attacker has approximately $2^{28} / 2^{256}$ chance, which is $2^{-228} \approx 2*10^{-69}$
  • For reference, finding a collision in SHA256 is: $4.3 * 10^{-60}$
  • Means, finding $p'(X)$ is around $10^{9} / 2 = 500000000$ times harder than finding a collision in SHA256… Wow!
• now that we proved $p(X)$ cannot be changed after being committed on, let’s inspect the other parts of this relationship → $\frac{p(X) - y}{X - z} = q(X)$
• $z$ cannot be changed, since the verifier herself send it, she would know…
• $y$ cannot be changed. Why?
  • assume otherwise. The prover wants to cheat with another value $y' \neq y$.
  • recall $p(z) - y = 0$,
  • then, $p(z) - y' \neq 0$ (remember, $y' \neq y$)
  • the prover needs to divide $p(X) - y'$ with $X - z$ in order to find $q(X)$.
  • But the prover cannot divide $p(X) - y'$ with $X - z$ , since $p(z) - y' \neq 0$.
  • if the prover can find a fake $q'(X)$, such that $q'(X) = \frac{(p(s) - y')}{s-z}$, then he can have the following relationship: $q'(s)(s-z) = p(s) - y'$
  • which is equivalent to $(\frac{(p(s) - y')}{s-z})(s-z) = p(s) - y'$,
  • which is equivalent to $p(s) - y' = p(s) - y'$, which will hold :)
  • but this cannot be done, since the attacker has to know about $s$ to compute $q'(X) = \frac{(p(s) - y')}{s-z}$. As long as $s$ is kept secret, we don’t need to worry about this.

---

Finalizing our proof with Kate Commitment

Let’s recall our relationship:

$$p(s) - y = q(s).(s-z)$$

And remember, we cannot work directly with this relationship, because both the prover and the verifier does not know $s.$ What do they know is, $\left[ s^i \right]$. And seems like that is enough!

The proof evaluation will work as the following:

$$\left[ q(s) \right] . \left[ s - z \right] = \pi . \left[ s - z \right] = C - \left[ y \right]$$

$\left[ q(s) \right]$ is our proof $\pi$.

What we’ve done is, we used $\left[ s^i \right]$ values to turn our equation into points in the elliptic curve.

So if we multiply $\pi$ with $\left[ s - z \right]$, and check that if equals to $C - \left[ y \right]$, we should be good to go for this scheme! And remember, all these are points on the elliptic curve.

However… there is one issue… we cannot multiply elliptic curve points :’)

To simulate this multiplication, we will use something called pairing.

---

Elliptic Curve Pairing in a nutshell

Pairing is an abstract definition, which will help us to multiply (kind of) two different elliptic curve points. A very basic (and probably wrong) summary could be useful to make it more tangible for our brains:

$$e(Q,P) = O$$

where Q and P are some points on the elliptic curve, and O is an integer (or a complex number) in the multiplicative group. Basically, we “multiplied” Q and P, and get a result of O.

Feel free to treat this as a black box and skip the next section if you are not a math nerd. Otherwise, below is a more elaborate explanation of pairing, enjoy!

Pairing (math warning! skip this if you want to treat it as a blackbox)

---

Pairing is a bilinear mapping.

What is a bilinear?

Linearity (the property of preserving linear combinations) exists for 1d functions such as $f(r)$, if that function obeys:

$$f(ar1+br2)=af(r1)+bf(𝑟2)$$

For 2d functions such as $f(r,s)$, the linearity attribute can exist for one dimension, or the other, or both. If both, then the function is said to be “bilinear”

$$f(ar_1+br_2,s)=af(r_1,s)+bf(r_2,s)$$ $$f(r,as_1+bs_2)=af(r,s_1)+bf(r,s_2)$$

What is bilinear mapping?

In mathematics, a bilinear map is a function combining elements of two vector spaces to yield an element of a third vector space, and is linear in each of its arguments. In plain english, we define a function that is taking two elements from different space, and producing an element in another third space.

Coming back to pairing:

This is a pairing: $e(Q, P)$

Pairing is an abstract operation. Abstract, because the definition can vary. There is Tate pairing, Weil pairing, Ate pairing, and so on… Each of them defining the pairing via different operations.

However, the format of the input and output, and the properties of the pairing is fixed.

• Input: 2 points ($P$ and $Q$) on 2 subgroups of the same curve ($\mathbb{G}_1$ and $\mathbb{G}_2$).
  • $\mathbb{G}_1$ is a subgroup of points for the elliptic curve, which in the form $y^2 = x^3 + b$, and both $x$ and $y$ are simple integers ($x,y ∈ F_p$ )
  • $\mathbb{G}_2$ is another subgroup of points for the same elliptic curve above (points satisfy the same equation as $\mathbb{G}_1$), but both $x$ and $y$ are elements of supercharged complex numbers ($x,y ∈ F_{p^{12}}$ ). $x$ and $y$ are in the format of $w^{12} - 18 * w^6 + 82 = 0$
• Output: an integer (or a complex number) in the multiplicative group $\mathbb{G}_T$ of order $n$.

In a crypto setting pairing should embody the following properties:

• $$e(P, Q + R) = e(P,Q) * e(P, R)$$
• $e(P + S, Q) = e(P,Q) * e(S, Q)$ (this is actually the same as above, I wanted to include it for verbosity)
• $e(aP, bR) = e(P,R)^{ab} = e(P, bR)^a = e(aP, R)^b = e(bP, aR)$ (simply, coefficients are interchangeable, because it is bilinear).
  • Notice that the coefficients are turning into exponents here if they move out of the parenthesis, unlike remaining as coefficients in the regular bilinearity description I gave above. The reason is, in the regular description, the inputs to the function, and the result, were all in the same format (they were assumed to be defined as an additive group). However, in here, the inputs are elliptic curve coordinates (which are additive), and the result is in $F^{q}_*$ format (a multiplicative finite field). To further explain, a multiplication operation for an additive group, is the same as an exponentiation for a multiplicative group. If you felt like this is too much math, unfortunately I agree…
  • I’ve encountered some other notations on this, in which, $\mathbb{G}_1$ and $\mathbb{G}_2$ are also defined as multiplicative groups. So the property turned into this: $e(P^a, R^b) = e(P,R)^{ab} = e(P, R^b)^a = e(P^b, R)^b = e(P^b, R^a)$. In short, this is some notation difference and it does not matter as much.
• $e(P, Q) ≠ 1$ (non-degeneracy property)
• additionally for cryptography → we also want this $e$ operation to be computable in an efficient manner.

---

Coming back to Kate proofs

Recall: Let $\mathbb{G}$ be the points on our elliptic curve, and $G$ be the generator of $\mathbb{G}$. Then, $\left[ x \right]$ is defined as → $\left[ x \right] = xG$. In other words, $\left[ x \right]$ converts $x$ to a point in the elliptic curve (corresponding to one of the points in $\mathbb{G}$).

Now we change it as the following:

• Let $\mathbb{G}_1$ and $\mathbb{G}_2$ be two different subgroups of the same elliptic curve
• $G$ be the generator of $\mathbb{G}_1$, and $H$ be the generator of $\mathbb{G}_2$,
• Then, $\left[ x \right]_1$ is defined as → $\left[ x \right]_1 = xG$
• And, $\left[ x \right]_2$ is defined as → $\left[ x \right]_2 = xH$
• Lastly, lets define our pairing $e: \mathbb{G}_1 \times \mathbb{G}_2 \rightarrow \mathbb{G}_T$, where $\mathbb{G}_T$ is the multiplicative target group

Of course, from the secret value $s$, now two different sets will be distributed, one for $\left[ s^i \right]_1$, and one for $\left[ s^i \right]_2$

Verifier should now check the equality of:

$$e(\pi, \left[s-z\right]_2) = e(C - \left[ y \right]_1, H)$$

which is equivalent to

$$\left[ q(s).(s-z)\right]_T = \left[ p(s) - y \right]_T$$

to which, we are very accustomed to by now :)

Verifier is able do the computations:

• $\left[ q(s) \right]$ is provided to verifier from the prover
• $z$ is selected by the verifier
• the verifier can compute $\left[s-z\right]_2$, since she has access to $\left[s \right]_2$, and computing $\left[s-z\right]_2$ is equal to computing $\left[s\right]_2 - \left[z\right]_2$
• $C$ is provided to her from the prover
• she also knows the value $y$ (sent by the prover)
• $H$ is public
• pairing function is public

The full workflow:

1. using a MPC setup, the secret $s$ is generated, and using this secret value, two sets will be distributed publicly, one for $\left[ s^i \right]_1$, and one for $\left[ s^i \right]_2$ . The secret $s$ is then discarded forever.
2. the prover selects a polynomial, and commits to it: $C = \left[ p(s) \right]_1$, using $\left[ s^i \right]_1$, and sends this to the verifier
3. verifier asks for the evaluation of the committed polynomial at point $z$
4. prover sends the following to the verifier:
   1. $$\pi$$
   2. $$y$$
5. verifier checks the equation: $e(\pi, \left[s-z\right]_2) = e(C - \left[ y \right]_1, H)$
   1. if equation holds, verifier accepts the proof
   2. if equation does not hold, verifier rejects the proof

We just showed how to prove an evaluation of a polynomial at a single point, using only one element as the proof! Using Merkle proofs, we would have to send all the coefficients to the verifier to prove that $p(z) = y$

---

Batch-proofs (multi-proofs)

We can go even further! Let’s show how to evaluate a polynomial at ANY number of points and prove it, using still ONLY ONE element.

Say we want to prove the evaluation of $k$ points:

$$(z_0, y_0), (z_1, y_1), ..., (z_{k-1}, y_{k-1})$$

Using an interpolation polynomial, we can find a polynomial of degree less than $k$, that goes through all these points. Using Lagrange interpolation, we can compute this interpolation polynomial. I know this may sound advanced, and it is. Google and YouTube will be your friends for understanding how Lagrange interpolation works.

The formula for computing the interpolation polynomial is as follows:

$$I(X) = \sum_{i=0}^{k-1} y^i \prod_{\substack{j=0 \\ j \neq i}}^{k-1} \frac{X-z_j}{z_i - z_j}$$

Since our original polynomial $p(X)$ is passing through all these points, the polynomial $p(X) - I(X)$ will be zero at each:

$$z_0, z_1, ... , z_{k-1}$$

Thus, this polynomial will be divisible by:

$$z_0, z_1, ... , z_{k-1}$$

So we define our zero polynomial as:

$$Z(X) = (X - z_0)(X - z_1)...(X - z_{k-1})$$

Using the zero polynomial, we can again establish a similar relationship that we did before:

$$q(X) = \frac{p(X) - I(X)}{Z(X)}$$

We now define the Kate multi-proof for the evaluations of the points:

$$(z_0, y_0), (z_1, y_1), ..., (z_{k-1}, y_{k-1}): \pi = \left[ q(s) \right]_1$$

Notice that our proof is still a single element!

Some differences in this scheme:

• the verifier needs to compute $Z(X)$ and $I(X)$
  • for computing these, she is going to need the $k$ points.
• she also will compute $\left[ I(s) \right]_1$ and $\left[ Z(s) \right]_2$
  • for computing these, she needs the sets $\left[ s^i \right]_1$ and $\left[ s^i \right]_2$

The equation the verifier needs to check is as the following:

$$e(\pi, \left[Z(s)\right]_2) = e(C - \left[I(s)\right]_1, H)$$

which evaluates into:

$$\left[q(s) . Z(s)\right]_T = \left[p(s) - I(s)\right]_T$$

And via this, we just proved the evaluation of ANY number of points on our polynomial, again providing a single element as a proof!

---

Kate as a vector commitment

It is actually quite easy to convert Kate polynomial commitment into a vector commitment. And via doing this, we will achieve the following:

• instead of sending $\log{n}$ hashes to prove a single element belongs to the vector, we will send only one element!
• our proof will consist of only one element, regardless of the vector size!

Here is how:

Previously, we were creating a polynomial using our data points as the coefficients. Now, we will do something different: say we have the elements:

$$a_0, a_1, ... , a_{n-1}$$

And say $p(X)$ is the polynomial that will evaluate to these elements as the following: $p(i) = a_i$.

So, for example, to reach $a_2$, we will plug in the value $2$ to our $p(X)$. We know there always is a polynomial that is passing though the points we like. Again, Lagrange interpolation will help us:

$$p(X) = \sum_{i=0}^{n-1} a^i \prod_{\substack{j=0 \\ j \neq i}}^{n-1} \frac{X-j}{i - j}$$

Using this polynomial, we can prove the presence of ANY number of elements in the vector using a SINGLE element!

p.s. thanks to Dariia Porechna for reviewing and contributing to this!

Resources:

• https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html
• https://hackmd.io/@tompocock/Hk2A7BD6U
• https://vitalik.ca/general/2017/01/14/exploring_ecp.html
• https://en.wikipedia.org/wiki/Bilinear_map
• https://math.stackexchange.com/
• https://crypto.stackexchange.com/