---

What is it good for?

One word: Authentication

Imagine you want to deliver a message in a network with Gossip Protocol. Between the recipient and you, say, there are 5 intermediate people who will relay your message. How will you know these intermediate people will not tamper with your message? Or worse, how will you know somebody else will craft a message on your behalf?

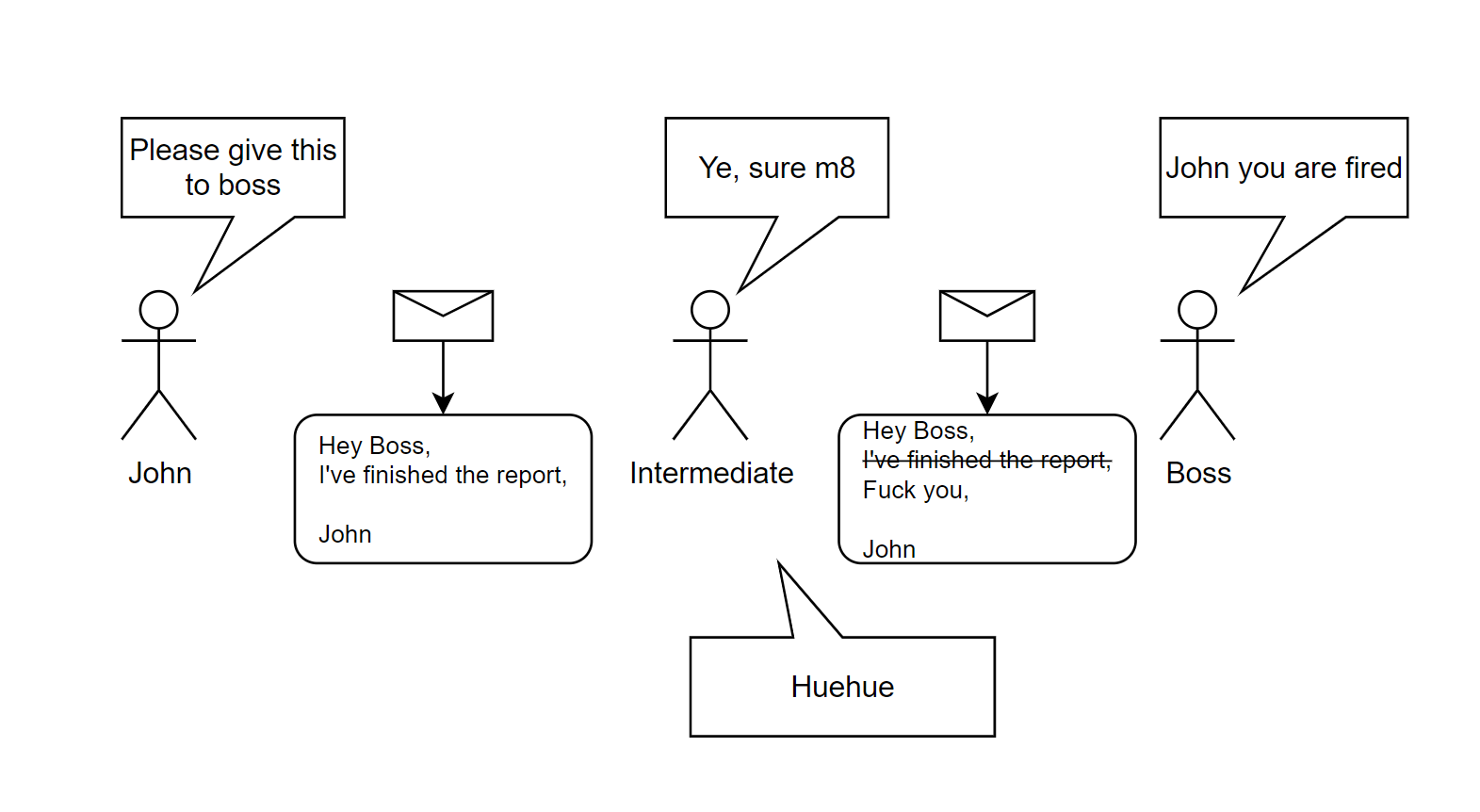
You can, by signing your message. So that, the recipient will discard the messages that do not possess your signature.

If you have little to no idea on how digital signatures work, you might be thinking that “what if they copy my signature as well? How can this be secure?”.

You shouldn’t think of digital signatures as the digitalized version of your signatures. Your physical signature stays the same for every message; digital signatures will change for every message, hence, copying them will not be useful.

Me

---

How it works?

Remember from public key cryptography each person will have a public and private key in PKC. For Digital Signatures, we will use RSA (maybe the most famous PKC algorithm). But do not worry, I have the perfect analogy for this, and you can understand how it works, even without math.

Think of a box, which has a lock. Instead of 1 key to control that lock, imagine we have 2 keys. One of these keys can only turn in clockwise in the lock (by design), and the other one can only rotate in anti-clockwise direction (again, by design).

Let’s make it more simple, we will refer to clockwise direction with +, anti-clockwise with -.

Our 2 keys are of course our private key and our public key.

Say private key can only make the lock turn in - direction, whereas public can make the lock turn in + direction.

Notice that, I did not say private key locks, public key unlocks, or vice versa.* They both can lock and unlock. This is very important.

Box is locked: lock is not at position 0 (it should be either + or - to be locked).

Box is unlocked: lock is at position 0 (neither - or +).

Let’s move on, and put some secret messages in our magical box. Then, turn the lock in - direction with our private key. Anybody who has access to our public key can turn the lock in + direction, effectively unlocking it.

This scenario might be sounding stupid, why encrypt something if it can be unlocked with everyone? Just send the plaintext instead… Duh!

Well, in fact, it is ingenious! Let’s discover why.

In order to sign a message, we will send 2 copies of the same message. One of them will be plaintext, everybody will be able to read it, there will be no modification to it at all. The second copy will be the encrypted version of the same message (with our private key, so turn the lock in - direction). Since we are the only one with our private key, nobody can turn the lock in - direction, but us. This is a proof of our Identity. When anybody received our message (consisting of 2 copies, one: plaintext, the other one: encrypted), they can decrypt our encrypted message with our public key (turning the lock in + direction, making the lock back into position 0), and check that the plaintext is the same with the decrypted text. If so, it is indisputable that we send the message, and nobody else did tamper with it.

Solution:

1. sender crafts $M = message \mathbin\Vert E_{private}(message)$
2. sender broadcasts $M$
3. recipient receives $M$
4. recipient checks if $message = D_{public}(E_{private}(message))$

Note: Both private and public keys displayed in the above equations belong to the sender.