---

What is it good for?

Remember from Symmetric Key Cryptography, both parties need to have the same keys in order to communicate with each other securely. But there is a problem, how can they decide upon the keys without letting an eavesdropper listen to the conversation. And remember, at this point, they are not encrypting their messages, since we need keys for encryption, and agreeing upon which key to use is the main problem.

Someone can easily listen to your conversation on the internet, there is nearly no perfect solution against this (we cannot prevent other people from listening to our conversations). But we can encrypt our messages, and even if they receive our messages, they cannot decrypt them without the necessary keys, rendering this malicious activity useless.

Coming back to our main problem, how can 2 parties (namely Alice and Bob) agree upon a secret key, without letting an eavesdropper (Eve) learn about this secret key? Public Key Cryptography is the magic, that solves this problem.

In short, Alice and Bob can securely agree upon a secret key, and the eavesdropper Eve cannot learn the value of secret key, even if she is listening to the communication.

---

How it works?

I can directly give you the technical definitions and math equations, which will prove that the system works. But probably you wouldn’t understand WHY is it working.

So, let’s start with a high-level abstraction. Say, our keys will be represented by colors. And in this fantasy scenario, Alice has the color(key) RED, whilst Bob has BLUE. They keep these colors(keys) to themselves, in other words, these are private keys. Private keys are meant to be private, you never share them.

Don’t ever share your secret keys

Anyone with a brain

So, Eve does not know about Alice has RED. and Bob has BLUE, since this private information is not being communicated.

Although not being helpful to our case, notice that Alice is fatter than Bob.

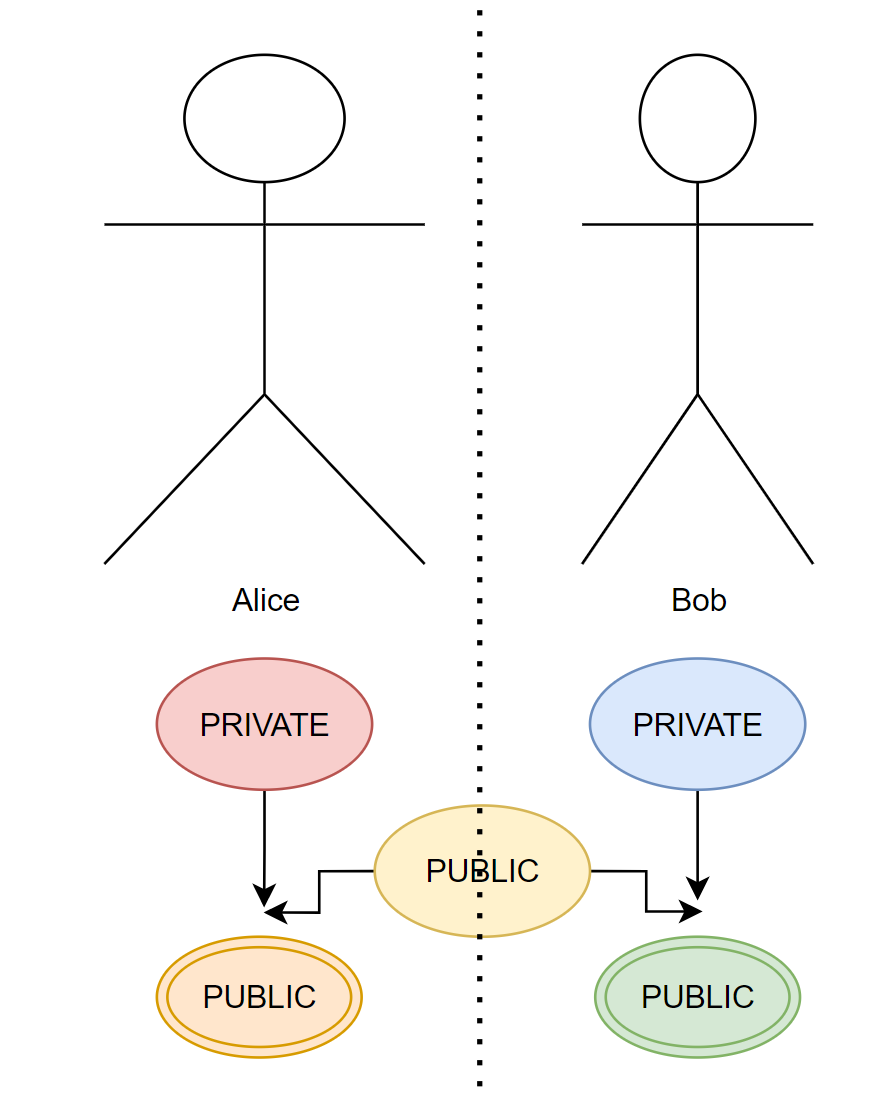
Now, both Alice and Bob, agree on a new random color, YELLOW. If you are a smartie, and asking the question “BUT EVE WILL LEARN ABOUT YELLOW!!”. Yes, Eve (who is eavesdropping) can learn about this YELLOW, it’s okay :)

This YELLOW is representing the public key, which means, everybody can know about it, there is no privacy for this information.

As the next step, Alice will cover her private key, with the public key (she will simply mix the colors RED and YELLOW together, achieving an orangey color. Bob will do the same, mixing YELLOW and BLUE together, ending up with a greenish color.

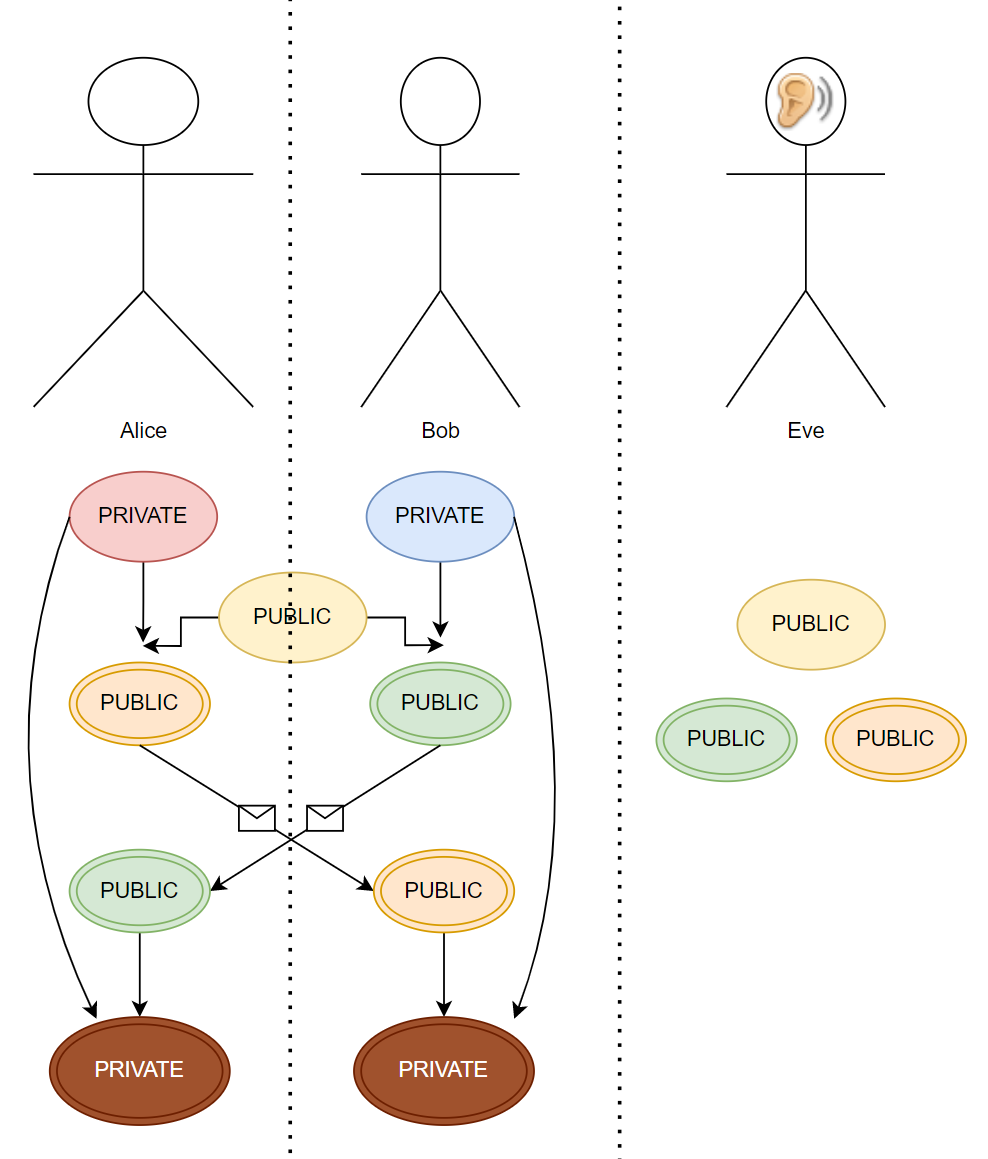
We are almost there! Now, Bob and Alice will send these mixed-up colors (orangey for Alice, greenish for Bob) to each other. Again, Eve can learn about these messages, since we are assuming that she is able to listen to the conversation.

And it’s done! Bob will use his private key (BLUE), to mix with the orangey color that Alice sent, and will end up with a disgusting color probably (brownish). Also, if Alice mixes her private key (RED) with the greenish color Bob sent, she will achieve the exactly same disgusting color as well. Why? Because BLUE + RED + YELLOW = brownish. Both Alice and Bob has the same ingredients for the final color! They will do these final mixing on their own, without telling anybody, so Eve will not learn about this process.

What did we get? Alice and Bob now have access to a key (that brownish color), which is secret, and hidden from Eve. They can use this key to apply Symmetric Key Cryptography for their communication from now on.

---

Color Analogy’s Inaccuracy

Although color-key metaphor is brilliant, it is inaccurate at one point. Consider this: if Eve knows the public key YELLOW, and she also knows that Alice sent orangey color to Bob, can’t she figure out Alice has RED?

The answer is: YES. And that’s why, we are not using colors, but math.

---

High Level Summary

There are 2 magical aspects of Public Key Cryptography (that we will achieve with math in the next section):

1. one-way functions, that prevents Eve to backtrack the color RED from YELLOW(public information) and the orangey(Alice’s public key) color.
2. although Bob do not know the color RED, she can still somehow use it in the mixture and get the brownish color. Remember: BLUE + RED + YELLOW = brownish

The above points are quite unintuitive, and hard to believe at first. But it is the reality, and math allow us to achieve these properties.

After here, it will get mathematical, if you are not interested in the technical details, and convinced upon how the public key cryptography works as an idea, feel free to skip the below part altogether, and confidently claim that you know how public cryptography works, in a sophisticated talk, just by explaining it with colors. I’m not kidding.

Math

Let’s identify the problem, we need a function, that Alice can compute ORANGE from RED and YELLOW easily, but Eve cannot compute RED from ORANGE and YELLOW easily. Probably you remember our encryption and decryption functions from Symmetric Key Cryptography.

$$encryption \rightarrow f(x, s) = x+s = y$$ $$decryption \rightarrow f^{-1}(y,s) = y-s =x$$

We are going to develop something really similar:

$$easy \rightarrow f(red, yellow) = orange$$ $$hard \rightarrow f^{-1}(orange,yellow) = red$$

The difference is, both the encryption and decryption were easy to perform in Symmetric Key Cryptography if you know the inputs. In this case, we want the hard function to be infeasible (Eve cannot compute it). A popular one-way problem is prime factorization. If I were to give you 2 prime numbers (say, $p$ and $q$), you can multiply them, and get their multiplication (say $n$) without any difficulty.

$$pq = n$$

Yet, if I were to give the $n$, and want you to find me $p$ and $q$, then your best chance is to brute-force, trying all the combinations one by one, without any efficient algorithm. On top of that, if $p$ and $q$ are large numbers (I mean 49048569048509823487234568947 is kind of large), good luck to you finding $p$ and $q$ before humanity extinct.

$$easy \rightarrow f(p, q) = n$$ $$hard \rightarrow f^{-1}(n) = p, q$$

This is all amazing and great. But how will it help us?

If you feel lost on how you can utilize prime factorization for the color analogy I made above, you are not alone. In the color metaphor, Eve had to compute the hard function, which has 2 inputs (ORANGE, YELLOW), and 1 output(RED). In prime factorization however, we are asking Eve to compute 2 outputs (ORANGE and RED?) with a single input(YELLOW). It’s not compatible! Eve already knows more than 1 input.

$$hard \rightarrow f^{-1}(orange,yellow) = red$$ $$hard \rightarrow f^{-1}(n) = p, q$$

Well, yeah… Prime factorization will not solve our problem. The reason I explained prime factorization is, it is easy to understand for all the audience, knowing the 4 basic operations (addition, subtraction, multiplication, division) is enough to understand prime factorization. And prime factorization is the simplest example to destroy the prejudice against how can a one-way functions exist?

Don’t worry, there exists a one-way function, which fits our scheme: Discrete Logarithm Problem. Say $g$ is a random integer, and we have a secret input $x$. And keep in mind that we will do all our operations in modulo $n$ in this setting.

If I raise $g$ to the power of $x$ in modulo $n$, I will get a new integer $h$. This is easy to compute.

$$h = g^x mod n$$

But if I provide you with the values of $g$ and $h$ (everybody knows $n$ in this setting, it is implicit, and no need to give it to you personally), and ask you to compute $x$, this will be really hard.

$$easy \rightarrow f(g, x) = h$$ $$hard \rightarrow f^{-1}(g, h) = x$$

---

Mapping Discrete Logarithm to Color

Let’s map the discrete logarithm problem to our color analogy.

public information in color analogy:

• yellow (public information)
• orangey (Alice’s public key)
• greenish (Bob’s public key)

private information in color analogy:

• red (Alice’s private key)
• blue (Bob’s private key)
• brownish (Alice and Bob’s shared secret key)

And we want to have the below functions:

$$easy \rightarrow f(red, yellow) = orangey$$ $$hard \rightarrow f^{-1}(orangey, yellow) = red$$

We had these in Discrete Logarithm Problem:

$$easy \rightarrow f(g, x) = h$$ $$hard \rightarrow f^{-1}(g, h) = x$$

So, it’s easy to map these now:

• the output of the hard function is red, which is Alice’s private key. This should be x.
• the output of the easy function is orangey, which is Alice’s public key. This should be h.
• the common input in both hard and easy functions is yellow. This should be g.

Good! Wait… What about n? We don’t have n in our color analogy. It’s ok though. n is public, which means, imagine there is an additional color in the analogy, that everyone knows about. If we want a more realistic analogy, we should modify the analogy by introducing another color along with yellow, and including this color for every mixture that will be made. This will be just meaningless in the color analogy, hence I left it out in the beginning. Analogies should be as simple and plain as possible. Let’s not further diverge from the topic, and continue to the math.

1st Step: Generating Public Keys

We actually already covered this. The Discrete Logarithm is:

$$h = g^x mod n$$

So, speaking from Alice’s perspective, she will generate her public key by raising g (yellow) to the power of her private key x (red) in modulo n (a new color). And she will arrive at h (orangey).

Bob will do the same. Only, x will represent blue, and h will represent greenish for Bob’s case.

2nd Step: Generating Shared Secret Key

This part is really fun, because it doesn’t require much math, but demanding analytical thinking skills. And the color analogy will help us a lot on the way.

Let’s remember how both parties arrive at the same brownish color, and let’s analyze it from the perspective of Alice.

Alice received greenish from Bob, and added her red to it.

greenish + RED = brownish

Where, in fact, greenish is just blue + yellow:

(BLUE + YELLOW) + RED = brownish.

And now, let’s do Bob:

Bob received orangey from Alice, and added his blue to it.

Where, in fact, orangey is just red + yellow:

orangey + BLUE = brownish

(RED + YELLOW) + BLUE = brownish

One potential pitfall: the + operator in the color analogy is not actually addition, it is representing the mix operation. In our math setting, the mix operation is $g^x mod n$.

Here is where we need to pay attention. The both equations are equal:

(RED + YELLOW) + BLUE = brownish

(BLUE + YELLOW) + RED = brownish.

And what you learned in your elementary school math is paying off now. This is the associative property of addition.

$$(a + b) + c = a + (b + c)$$

In other words, our operation for mixture (Discrete Logarithm) should have associative property as well in order for this scheme to work.

The good news is, it does! $(g^x)^y mod n = (g^y)^x mod n$

The above equation may be hard to digest, so let’s map it back to our color analogy.

$$g^x mod n = yellow + red = orangey$$ $$g^y mod n = yellow + blue = greenish$$ $$(g^x)^y mod n = orangey + blue$$ $$(g^y)^x mod n = greenish + red$$

Voila!

In summary, we found such a mathematical operation, that has the following properties:

• it is a one-way function: provides security for eavesdropping
• it has associative property: allows Alice and Bob to achieve the same result by different order of operations
• it is somewhat homomorphic: hides the private keys (red and blue colors), yet somehow allows using them in the mathematical context without revealing them. $(g^y)$ is used by Alice, but Alice still does n know what y is, and yet she can compute $(g^y)^x mod n$, which is equivalent to $(g^x)^y mod n$, and in this form the y part seems to be exposed, but it is actually not. It is still not possible to compute y from $(g^x)^y mod n$.

The Whole Scheme In Action

Setup Phase

Public Parameters:

• n = 13 (this actually has to be a prime number due to modular arithmetic constraints, and usually denoted as p, just a side note for the curious)
• g = 2

Private Parameters:

• Alice chooses a private key a = 4
• Bob chooses a private key b = 6

Public Key Generation Phase

• Alice’s public key: $A = g^a mod n = 2^4 mod 13 = 16 mod 13 = 3$
• Bob’s public key: $B = g^b mod n = 2^6 mod 13 = 64 mod 13 = 12$

Key Exchange Phase

• Alice sends A to Bob
• Bob sends B to Alice
• Eve can learn about A and B, it’s completely ok.

Compute The Shared Secret Key Phase

• Alice computes $s = B^a mod n = 12^4 mod 13 = 20736 mod 13 = 1$
• Bob computes $s = A^b mod n = 3^6 mod 13 = 729 mod 13 = 1$

Conclusion

Alice and Bob did not share their private keys with anyone, yet they were able to compute the same secret key. And Eve, the eavesdropper, was not able to derive any of the secret information:

• private key of Alice
• private key of Bob
• the shared secret key

Thanks for reading!